Want to explore how rheology can help with your stability investigations?
Creaming, sedimentation, flocculation and coalescence: four clear signs that spell failure for a formulation. Stability is one of the fundamental properties of an emulsion, if the product doesn’t remain emulsified then no claims of its youth-enhancing or taste-bud-tantalizing properties (emulsions are used in so many ways!) will matter.
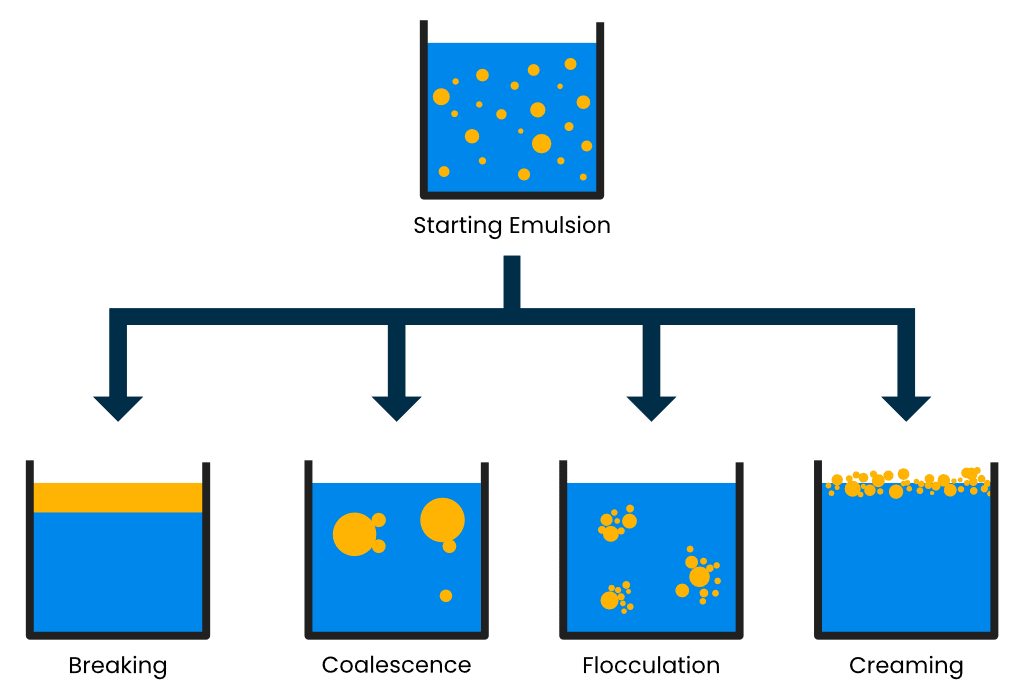
Predicting long-term stability using one quick test is the Holy Grail for anybody formulating emulsion products; rheology alone cannot provide this but it can offer an immediate indication of potential trouble ahead. The most useful information regarding stability can be gathered using very gentle tests to analyse emulsions under very low stress conditions that simulate those on storage.
Zero-shear viscosity: Storage viscosity or “Shelf” viscosity
The concept of non-Newtonian flow is often the first thing people learn when first entering the world of rheology. The use of simple single-speed Brookfield-style viscometer measurements suggest viscosity is a single number for any given liquid but that’s very often not the case, and certainly not in the case of emulsions. For non-Newtonian liquids the viscosity depends on the shear conditions that the sample is currently experiencing. For non-Newtonian shear-thinning liquids, as the applied shear rate is increased the viscosity drops. The corollary of this is that, with lower and lower rates of applied shear, viscosity increases. However, for practical purposes, viscosity does not keep rising indefinitely with less and less movement but “tops-out” at a plateau referred to as the zero shear viscosity. Simply put this is the viscosity of the sample when under “creeping-flow” conditions, such as would be experienced, for example, during storage.
The practical value of zero-shear viscosity measurements is that they enable us to rapidly determine and quantify the “mobility” of an emulsion. A product with a high zero-shear viscosity would expect to have an impeded movement of droplets or flocs/aggregates of droplets, potentially prolonging shelf life through the inhibition of creaming processes and possibly through limiting interactions that may lead to coalescence.
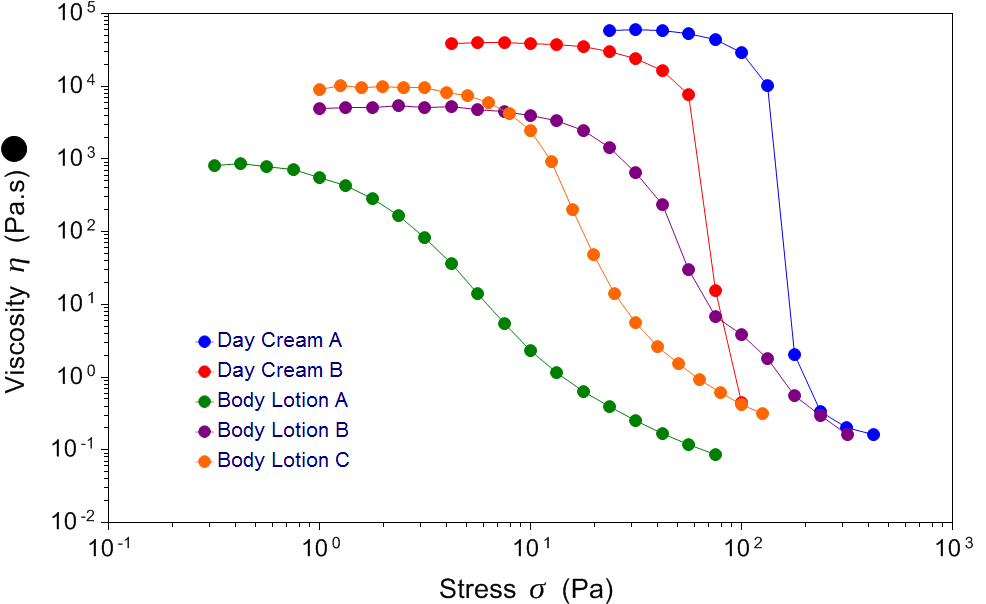
The example below shows very clear zero-shear viscosity plateaus spanning a wide range of viscosity for a selection of cosmetic emulsions. Body Lotion A demonstrates a plateau of around 1000 Pa.s (1 million centiPoise) whilst the zero-shear viscosity for Day Cream A approximates 70 000Pa.s (70 million centiPoise). The 70 x greater mobility of the lotion may manifest in a shortened long-term shelf life.
Stokes’ Law for settling or creaming
Stokes’ Law is an equation often employed to calculate the terminal velocity of either a particle settling in a less dense continuous medium, or, of a bouyant droplet rising through a more dense continuous medium. The equation’s application to real-life formulations is limited as it assumes “non-interacting spheres”, a condition clearly not present in our emulsions above. However Stokes Law can be instructive none-the-less.
Stokes’ Law states that the terminal velocity, V, in m/s, is given by:
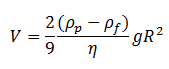
- g is the gravitational acceleration (m/s2)
- ρp is the density of the particles (kg/m3)
- ρf is the density of the fluid (kg/m3)
- η is the continuous medium viscosity (Pa.s)
- R is the particle or droplet radius (m)
The equation features a viscosity term for the continuous phase. In the case of a simple liquid this would be a Newtonian viscosity but, in the case of particles or droplets in a thickened liquid, where that thickening may be brought about by the presence of a dissolved polymer or gum, it would be more appropriate to measure the zero-shear viscosity of the continuous phase in isolation and then input that value into the equation.
You can learn more about zero shear viscosity here https://www.rheologylab.com/videos/zero-shear-viscosity/

If you would like any advice or assistance measuring zero-shear viscosity, or have any other suspension or emulsion questions, please contact us and we will be happy to help.
